La bellezza della matematica nel cervello
DIANE RICHMOND & PATRIZIO PERRELLA
NOTE
E NOTIZIE - Anno XII – 08 novembre 2014.
Testi pubblicati sul sito
www.brainmindlife.org della Società Nazionale di Neuroscienze “Brain, Mind
& Life - Italia” (BM&L-Italia). Oltre a notizie o commenti relativi a
fatti ed eventi rilevanti per la Società, la sezione “note e notizie” presenta
settimanalmente lavori neuroscientifici selezionati fra quelli pubblicati o in
corso di pubblicazione sulle maggiori riviste e il cui argomento è oggetto di
studio dei soci componenti lo staff dei
recensori della Commissione Scientifica
della Società.
[Tipologia del testo:
DISCUSSIONE/AGGIORNAMENTO]
È innegabile che il concetto di bellezza, fin dall’antichità classica, sia stato legato alla forma, alla sua armonia, ad elementi percepiti dalla vista in grado di evocare piacere, preferenza, desiderio. Le radici psicologiche millenarie di questa concezione sono evidenti quando si pensi alla formula degli antichi Greci che spiegava in cosa consista il senso e il potere della bellezza: una promessa di felicità.
Una sintesi suggestiva, che può far pensare ad una persona alla quale si desidera legarsi o ad un luogo da sogno dove trascorrere la vita; ossia una concreta esperienza percettiva che si presta ad essere idealizzata. In fondo, anche il moderno concetto di belle arti appartiene a questa tradizione, sia nell’epoca della rigorosa imitazione della natura, sia in quella delle astrazioni estetiche, fino alla dissoluzione di canoni e paradigmi tradizionali nella varie espressioni dell’arte contemporanea.
Nella storia non sono stati pochi i filosofi che hanno proposto l’esistenza di un senso profondo e universale della bellezza e dell’estetica, emancipato dall’esperienza diretta e particolare della percezione; si pensi, in epoca non lontana dalla nostra, alla concezione dell’estetica quale scienza filosofica della sensibilità, introdotta da Baumgarten, adottata da Kant e sviluppata nel pensiero dei due secoli successivi. Tuttavia, un tale modo di considerare l’esperienza del bello non ha creato opinione diffusa, così che la tesi sostenuta da vari matematici secondo cui la bellezza matematica non sarebbe diversa da quella musicale o figurativa, ha incontrato molte resistenze.
Semir Zeki[1], neuroscienziato fra i fautori della neuroestetica, ha provato a verificare la fondatezza neurobiologica della tesi sostenuta dai matematici, studiando il cervello durante un’esperienza di bellezza matematica, alla ricerca dei correlati neurofunzionali, per paragonarli a quelli individuati nel corso di esperienze estetiche convenzionali.
Per molti versi, questo studio non è paragonabile alle precedenti esperienze che hanno cercato di individuare la base del bello nel cervello umano. Infatti, la categoria culturale che corrisponde al valore estetico positivo di cui ciascuno può fare esperienza, indica tanto forme pressoché universali quanto realtà soggettive. La maggior parte dei gruppi di ricerca che ha affrontato il problema delle basi neurali della bellezza ha considerato la percezione di immagini unanimemente ritenute un’espressione evidente se non emblematica di questo valore. In altri termini, in una gamma continua fra soggettivo ed oggettivo, il bello dal quale si è partiti poteva collocarsi in vicinanza del polo oggettivo, come potenzialmente universale; mentre nel caso della bellezza matematica potrebbe collocarsi in prossimità del polo soggettivo.
Diamo ora uno sguardo d’insieme alla procedura e ai risultati ottenuti.
Guidati da Zeki, ricercatori provenienti da istituti inglesi e scozzesi, hanno sottoposto 15 matematici, in qualità di volontari, ad una prova consistente nel vedere e giudicare in termini estetici 60 equazioni. Per oggettivare le stime e poterle rapportare con precisione ai quadri morfo-funzionali cerebrali, è stato richiesto ai matematici di adottare una scala di punteggi con valori che andavano da un minimo di – 5 (la più brutta) ad un massimo di + 5 (la più bella).
Le scansioni in risonanza magnetica funzionale (fMRI) hanno consentito di visualizzare la risposta del cervello al riesame delle equazioni viste in sequenza.
Il follow-up è stato molto importante per discernere in relazione ad una tendenza inconscia che avrebbe potuto falsare i risultati: la comprensione e la conoscenza tendono a creare una preferenza (bias); pertanto, un’equazione già vista e compresa ha maggiori probabilità di essere prescelta e, dunque, di essere considerata bella. Nella ripetizione delle prove si è perciò fatta la tara di questa occorrenza rispetto al giudizio di bellezza. È emerso che la comprensione matematica era un requisito necessario ma non sufficiente perché un partecipante considerasse bella un’equazione: alcune, infatti, erano ben comprese ma non colpivano esteticamente i matematici.
Sulla base di questa differenza, si è individuato il primo correlato funzionale dell’esperienza del bello matematico in un’attivazione della corteccia orbitofrontale mediale. Questa regione è stata implicata nel processo decisionale, ma sembra avere un ruolo importante anche nell’integrazione dell’esperienza sensoriale e delle emozioni. Alcuni studi hanno rilevato e documentato che la corteccia orbitofrontale mediale è altamente attiva mentre una persona percepisce qualcosa come bella, indipendentemente dal fatto che sia una rappresentazione figurativa o un brano musicale.
Ma, consideriamo in dettaglio alcuni aspetti dello studio.
Fra le 60 formule proposte quella più frequentemente valutata bella dai matematici che hanno partecipato allo studio di Zeki è stata l’identità di Eulero:
![]()
Tale identità è un caso particolare dell’equazione nota come formula di Eulero, dimostrata per la prima volta da Roger Cotes nel 1714 e successivamente riscoperta, indipendentemente, dal matematico svizzero Leonhard Euler[2] che la rese famosa inserendola nella sua opera Introductio in analysin infinitorum, pubblicata nel 1748 a Losanna da Marcum-Michaelem Bousquet & socios[3].
Molti matematici concordano nel considerare questa formula straordinaria o, quanto meno, notevole per la semplicità con la quale collega quantità fondamentali appartenenti ad ambiti diversi della matematica. Si può osservare infatti che in essa sono presenti simultaneamente: l’elemento neutro dell’addizione (lo zero) e l’elemento neutro della moltiplicazione (l’unità) che sono, per così dire, espressione di concetti algebrici, l’unità immaginaria (la i) che invece appartiene al campo dei numeri complessi, la costante p che è fondamentale in trigonometria e geometria euclidea, la costante e che è più propriamente di ambito analitico. Essa inoltre mette insieme anche tutti gli operatori fondamentali dell’aritmetica: uguaglianza, addizione, moltiplicazione, elevamento a potenza; e ciascun simbolo in essa vi figura in un’unica occorrenza.
Si può quindi ritenere che i matematici tendano a considerare bella una tale formula sia per l’eleganza stilistica della sua formulazione sintattica sia per l’elevato valore semantico da essa espresso con estrema immediatezza, semplicità e leggerezza.
La formula che nello studio di Zeki è stata invece più frequentemente indicata come la più brutta è uno sviluppo in serie del reciproco di p dovuta al matematico indiano Srinivasa Ramanujan[4]:
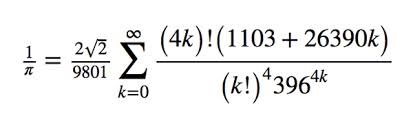
A differenza dell’identità di Eulero questa formula di Ramanujan contiene una sola costante notevole (p) del cui reciproco fornisce una rappresentazione e, al contempo, un metodo di calcolo approssimato. Il valore semantico di tale equazione è quindi decisamente molto meno elevato.
Dal punto di vista, invece, della formulazione sintattica si può notare in questa equazione la presenza di alcune costanti numeriche, prive di qualsiasi interesse teorico (i numeri 9801, 1103, 396, 26390) la cui eterogeneità compromette l’armonia estetica della formula stessa. Inoltre, la presenza di un fattoriale (!) sia a numeratore che a denominatore del termine di sommatoria, contribuisce ad appesantire la formula.
Concludendo, si propone una riflessione sul significato dell’attivazione della corteccia orbitofrontale mediale.
Sembra si dia per implicito, e tale è l’impressione che si desume anche dalla lettura dei commenti[5], che la condivisione di quest’area nello schema di attività rilevato indichi un’identità del senso fisiologico e del valore dell’esperienza. Se una tale possibilità, da un canto, non può essere esclusa, dall’altro non è nemmeno provata o desumibile con un grado elevato di certezza. Se le facoltà, le abilità e le funzioni intese in senso psicologico avessero un rapporto di corrispondenza biunivoca con una regione cerebrale, come ingenuamente supposto in passato dai frenologi, allora non vi sarebbero dubbi e discussioni. Ma, alla luce delle conoscenze attuali, si è autorizzati a supporre proprio l’opposto: ciascuna area anatomica corticale studiata, eccetto le aree motorie e percettive primarie, interviene nella mediazione di più funzioni, e le attività corrispondenti ad abilità o stati psichici sembrano sempre dipendere dall’elaborazione di reti di aree fra loro collegate.
Un’altra considerazione sulla corteccia prefrontale e, in particolare, sulla regione orbitofrontale mediale, accresce ulteriormente i dubbi: un elenco dettagliato dei processi nei quali la corteccia prefrontale è attiva, si risolverebbe in una lunga lista dalla quale ben poche facoltà mentali rimarrebbero escluse. Se l’ambito dei processi in cui è stato provato un intervento della corteccia orbitofrontale mediale è decisamente più circoscritto, il tipo di funzioni, andando dall’attività cognitiva di prendere delle decisioni all’elaborazione affettivo-emotiva, è tanto ampio ed eterogeneo da scoraggiare qualsiasi semplificazione. Pertanto, se la percezione del bello in un’equazione matematica, in una melodia o nel volto di una Madonna di Raffaello sono la stessa cosa, non ci sembra che la prova possa venire dal reperto dell’attivazione di quest’area cerebrale.
Infine, un aspetto che ci sembra rilevante è rappresentato dalla concezione del rapporto fra mente e cervello dei ricercatori che conducono uno studio: dal modo in cui si concepisce questa relazione dipende sia il senso dei quesiti che si pongono al vaglio sperimentale, sia il senso che viene attribuito alle risposte fornite dagli esiti della sperimentazione. Se si ritiene che i contenuti e l’identità di un’esperienza, come quella della bellezza, siano riducibili alla base neurofunzionale che ne media l’espressione, è comprensibile che individuato un correlato neurofunzionale lo si identifichi con il senso dell’esperienza stessa. Se, al contrario, non si ritiene che un’esperienza sia “niente altro che quei circuiti attivati”, ma abbia la sua identità in ciò che si prova soggettivamente e si rende in una intersoggettività estesamente condivisa e culturalmente codificata, non sarà la localizzazione nel cervello dell’area più attiva durante l’esperienza a dirci cosa questa sia e se sia uguale o diversa nella sua identità da altri stati psichici.
Gli autori della nota ringraziano
la dottoressa Isabella Floriani e invitano alla lettura delle recensioni di
argomento connesso che appaiono nella sezione “NOTE E NOTIZIE” del sito (utilizzare
il motore interno nella pagina “CERCA”).